¶ Résumé de l'atelier 7uring n°2
¶ Résumé du déroulé de l'atelier
L'atelier de cette semaine s'est articulé autour des points suivants :
- Présentation des différents types de problèmes rencontrés lors de compétitions d'algorithmie dont le SWERC.
- Un premier problème dont la difficulté réside sur une approche algorithmique optimale.
- Un second problème dont la difficulté réside plutôt sur sa modélisation/compréhension.
Par la suite on détaillera les points importants de cet atelier.
¶ Problème K: La création d'équipe
Le premier problème du jour était celui de : Créer deux équipes dont chaque représentant choisit à son tour un joueur. Pour ceci, chaque leader choisissait successivement le k-ième joueur parmi les joueurs restants.

Ce problème, d'apparence simple, revient à Trouver et extraire le k-ième élément d’une liste ordonnée. La difficulté réside donc à le résoudre à l'aide d'un algorithme efficace, puisque l'on peut avoir un nombre de joueurs allant jusqu'à 4 000 000 de joueurs.

¶ Méthodes de résolution proposées par les gens présents
Dans un premier temps, on pourrait modéliser la liste des joueurs par une
liste d'entiers représentant l'indice de chacun des joueurs.
Exemple (pour 16 joueurs disponibles):
# Liste énonçant si un joueur est disponible (0) ou déjà dans une équipe (1)
D = [1, 1, 1, 0, 1, 0, 0, 0, 1, 1, 0, 1, 1, 1, 1, 0, 1, 1]
# Liste des joueurs
J = [0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15]
- Un algorithme naïf consisterait donc à parcourir la liste des joueurs disponibles à l'aide de la liste
D. Or le problème ici est que l'on aurait une complexité temporelle en O(N²) car l'on devrait parcourir simultanément deux listes de taille N.
Si nous modélisons ce problème à l'aide de matrices ou tableaux, le parcours apportant une compléxité linéaire nous bloquerait et entraînerait une complexité au moins quadratique, alors comment faire ?
-
Le dictionnaires sont une collection de données ayant l'avantage d'avoir une complexité de parcours en O(1), ce qui résout notre problème précédent, mais ne nous fait pas avancer car pour sélectionner un joueur, nous devront toujours faire un second parcours pour vérifier s'il est disponible ou non.
-
La structure de données à privilégier ici serait donc l'arbre, structure arborescente dont nous avons de nombreux algorithmes à portée de main, et dont il y a beaucoup de structures dérivées (arbres binaires, équilibrés, tries,...).

Figure 1: Exemple d'un arbre binaire complet
Une des solution que nous allons souligner pour résoudre ce problème est l'utilisation d'arbres de segments.

Figure 2: Exemple d'un arbre de segments, arbre pour stocker des intervalles ou des segments
Pour modéliser des arbres de segments sur python, on peut s'aider de la classe suivante:
class SegmentTree:
def __init__(self, data, default=0, func=max):
self._default = default
self._func = func
self._len = len(data)
self._size = _size = 1 << (self._len - 1).bit_length()
self.data = [default] * (2 * _size)
self.data[_size:_size + self._len] = data
for i in reversed(range(_size)):
self.data[i] = func(self.data[i + i], self.data[i + i + 1])
def __delitem__(self, idx):
self[idx] = self._default
def __getitem__(self, idx):
return self.data[idx + self._size]
def __setitem__(self, idx, value):
idx += self._size
self.data[idx] = value
idx >>= 1
while idx:
self.data[idx] = self._func(self.data[2 * idx], self.data[2 * idx + 1])
idx >>= 1
def __len__(self):
return self._len
def query(self, start, stop):
"""func of data[start, stop)"""
start += self._size
stop += self._size
if start == stop:
return self._default
res_left = res_right = self._default
while start < stop:
if start & 1:
res_left = self._func(res_left, self.data[start])
start += 1
if stop & 1:
stop -= 1
res_right = self._func(self.data[stop], res_right)
start >>= 1
stop >>= 1
return self._func(res_left, res_right)
def __repr__(self):
return "SegmentTree({0})".format(self.data)
Voyons comment résoudre l'exemple du sujet avec cette modélisation:
Pour un nombre N = 4 de joueurs :
- trouver_i(Liste.data, 4) cherche le 4ème joueur disponible.
- Supposons qu'il retourne 3 (le joueur 4).
- Marque le joueur 4 comme pris : Liste.data = [1, 1, 1, 0, 1, 1, 1, 1].
- result = [4].
Pour N = 2 :
- Cherche le 2ème joueur disponible.
- Supposons qu'il retourne 2 (le joueur 2).
- Marque le joueur 2 comme pris : Liste.data = [1, 0, 1, 0, 1, 1, 1, 1].
- result = [4, 2].
Etc pour tous les éléments de a_retirer.
On obtient alors l'algorithme suivant:
# permet de trouver efficacement le i-eme élément qui n'a pas encore été pris
def trouver_i(tree, n, k=1):
if tree[k] < n:
return k, (n - tree[k])
if (2 * k + 1) > len(tree):
return k, n - tree[k]
k_g, n_g = trouver_i(tree, n, 2 * k)
if n_g == 0:
return k_g, 0
else:
return trouver_i(tree, n_g, 2 * k + 1)
liste = [1] * 8
Liste = SegmentTree(liste, func=(lambda x, y: x + y))
a_retirer = [4, 2, 5, 5, 4, 2, 1, 1]
result = []
for n in a_retirer:
a, b = trouver_i(Liste.data, n)
i = a - len(Liste)
result.append(i + 1)
Liste[i] = 0
# Pour plus de simplicité, on a pas représenté les 2 équipes
# On fait juste une seule liste pour tester en mettant tous les éléments
# retirés par les 2 chefs d'équipe dans l'ordre où ils ont été retirés
print(result)
# print(sorted(result))
Dans lequel dans l'ordre:
- On crée les éléments disponibles
- Chaque noeud stocke le nb d’éléments dispos
- Trouver l’indice de l’élément à retirer, marqué comme retiré en remplaçant par 0 dans Liste
- Ajouter l’indice de l’élément retiré au résultat
¶ Problème A: Le jeu de cartes
Le second problème du jour consistait à: Organiser la main d'un jeu de cartes de sorte à les avoir rassemblées par type et par ordre croissant, avec les atouts à la fin.
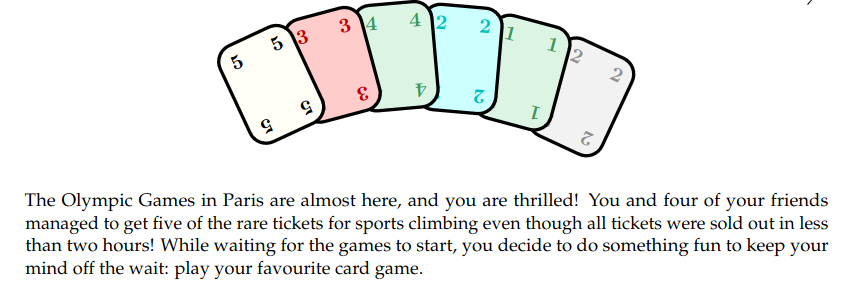
Pour ceci, nous disposons d'un jeu de cartes de 5 types différents {S, W, E, R, C} associés à 5 couleurs représentées ci-dessus. Nous nous intéressons au nombre minimal d'actions à faire pour trier ce jeu de cartes, sachant que deux cartes d'un même type doivent être triées selon leur numéro de façon croissante.

Exemple (pour 5 cartes):
# Entrée
5
S2 W4 E1 R5 C1
# Sortie
0
Exemple (pour 4 cartes):
# Entrée
4
C1 R2 E4 R1
# Sortie
2
¶ Méthodes de résolution proposées par les gens présents
La difficulté du problème réside dans un premier temps sur sa compréhension: on ne cherche pas à trier un ensemble de cartes mais à déterminer le nombre minimal de mouvements à faire pour le trier.
Pour ceci, essayons de comprendre les exemples pour trouver un algorithme déterminant un tel nombre.
Il est clair que pour le premier exemple la valeur de sortie soit nulle car les cartes sont déjà triées. Pour le second jeu, essayons de voir comment la valeur 2 a été trouvée en triant ces cartes en deux coups (N.B. un déplacement signifie bien-sûr une insertion):
C1 R2 E4 R1 ↓
C1 E4 R1 R2 ↓ # on déplace R2
E4 R1 R2 C1 # on déplace C1
Ou sinon:
C1 R2 E4 R1 ↓
R2 E4 R1 C1 ↓ # on déplace C1
E4 R1 R2 C1 # on déplace R2
Un autre exemple avec un peu plus de cartes:
C1 S3 E2 E1 R1 R4 W1 ↓
S3 E2 E1 R1 R4 W1 C1 ↓ # on déplace C1
S3 W1 E2 E1 R1 R4 C1 ↓ # on déplace W1
S3 W1 E1 E2 R1 R4 C1 # on déplace E2
Après plusieurs exemples, nous pouvons remarquer que pour trier les cartes en un nombre minimal de déplacements, on ne déplace jamais celles qui sont déjà en place, c'est-à-dire supérieures à la carte qui la précèdent ou inférieures à la carte qui la succèdent.
Pour aller plus loin, on ne déplace que les cartes qui ne font pas partie de la sous-liste croissante de la liste des cartes.
En effet: pour la liste C1 S3 E2 E1 R1 R4 W1 du dernier exemple, on a la plus grande sous-liste croissante suivante S3 E1 R1 R4 en supprimant C1, E2 et W1 qui brisent la suite.
Le nombre de déplacement minimal correspondant au nombres de cartes qui doivent être déplacées, on peut en déduire qu'il correspond à toutes les cartes qui ne font pas partie de cette sous-liste croissante maximale.
Autrement dit, il suffit de calculer la taille M de la sous-liste croissante la plus grande et le résultat du problème est alors N-M.
Il suffit pour cela d'utiliser un algorihme en O(nlog(n)) pour trouver une telle taille, et on obtient le code suivant proposé par le SWERC:
from itertools import permutations
from bisect import bisect
class Card:
suit: str
number: int
def __init__(self, S: str):
assert S[0] in set("SWERC")
self.suit = S[0]
self.number = int(S[1:])
assert 1 <= self.number <= N
def convert_to_number(self, order_on_suit):
# pour comparer des cartes encodées par une lettre et un entier,
# on peut les convertir en entier comme ceci par exemple
return self.number - 1 + N * order_on_suit[self.suit]
def length_longuest_increasing_sequence(l):
end_lis = []
for value in l:
pos = bisect(end_lis, value)
if pos == len(end_lis):
end_lis.append(value)
else:
end_lis[pos] = value
return len(end_lis)
# Parse input
N = int(input())
assert 1 <= N <= 100000
hand = [Card(s) for s in input().split()]
assert len(hand) == N
min_moves = N
for perm_on_suit in permutations(list("SWER")):
order_on_suit = {suit: i for i, suit in enumerate(perm_on_suit)}
order_on_suit["C"] = 4 # trump card is always last
ordered_hand = [card.convert_to_number(order_on_suit) for card in hand]
lis = length_longuest_increasing_sequence(ordered_hand)
if N - lis < min_moves:
min_moves = N - lis
print(min_moves)