¶ Résumé de l'atelier 7uring n°1
¶ Résumé du déroulé de l'atelier
L'atelier de cette semaine s'est articulé autour des points suivants :
- Présentation de 7uring
- Présentation des compétitions d'algorithmie (SWERC, Prologin…)
plus d'info sur la page publique de 7uring - Problème de résolution d'un labyrinthe
Réflexion ensemble à plusieurs solutions
Temps laissé aux gens pour essayer d'implanter un algorithme à base de backtracking - Correction possible pour le labyrinthe
- Présentation du crible d'érathosthène pour lister des nombres premier
- Bonus : Réflexion sur la représentation des matrices
Par la suite on détaillera les points importants de cet atelier
¶ Problème du Labyrinthe
Le problème du jour était celui de : Trouver un chemin permettant de résoudre un labyrinthe. On se moquait de trouver un chemin particulier du style « Chemin le plus court, Chemin demandant le moins de virages, le plus rapide… », seul nous importait que le chemin permette d'atteindre la sortie.
Le labyrinthe dans cet exercice est une matrice de murs et d'espaces libres dont l'entrée est toujours la case en haut à gauche et la sortie toujours celle en bas à droite. Les cases en dehors du labyrinthe sont considérées inaccessibles.
Exemple :
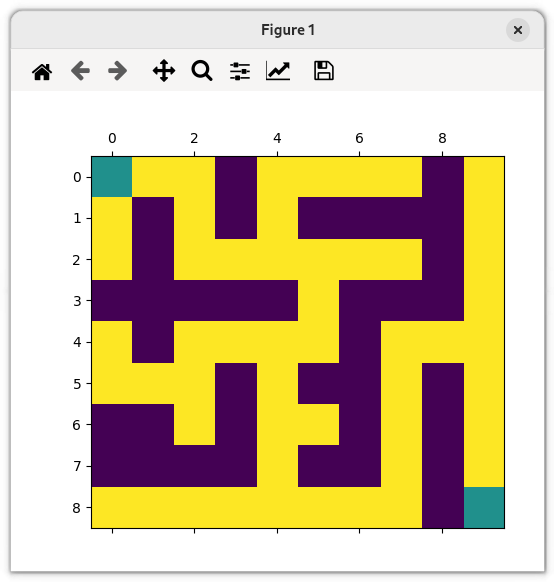
- en vert : les cases départ et arrivée
- en jaune : les cases libres
- en violet : les murs
¶ Méthodes de résolution proposées par les gens présents
Quatre principales méthodes on été proposées pour résoudre ce problème :
- Affecter à chaque case libre, un entier correspondant à sa distance à la sortie. Cela correspond à créer un champ scalaire des distances, puis d'emprunter le chemin à partir de l'entrée du labyrinthe en suivant les plus petites valeurs de distance.
Cet algorithme peut s'apparenter à un cas particulier des algorithmes de plus court chemin, ne nécessitant pas de construire explicitement le graphe associé au labyrinthe (voir 2.). - Considérer le labyrinthe comme un graphe non orienté (chaque case étant un nœud de ce graphe, puis appliquer un algorithme du plus court chemin comme Dijkstra. Chaque nœud (les cases libres) serait relié à ses cases libres adjacentes.
Les algorithmes de « pathfinding » (recherche du plus court chemin) sur les graphes seront probablement étudiés dans un futur atelier de 7uring donc on ne détaillera pas cette solution. - Algorithme « naïf » : suivre toujours le mur de droite (ou de gauche). Cet algorithme permet d'exhiber une solution (généralement pas optimale contrairement à précédemment). Cet algorithme est beaucoup plus simple à comprendre et est moins coûteux que les solutions précédentes dans le cas où on ne cherche pas de solution particulière.
ATTENTION toutefois : Il faut bien penser quand on programme cet algorithme à garder en mémoire l'orientation à chaque instant de notre personnage virtuel qui parcourt le labyrinthe. Sinon on risque de tomber dans le piège de faire un algorithme qui fait une boucle infinie au premier cul-de-sac. - Algorithme à base de backtracking. C'est la solution que nous allons détailler au paragraphe suivant.
Un bon exercice est d'écrire l'algorithme de la main droite ou les propositions 1. et 2., on ne donnera pas de correction ici, mais n'hésitez pas à envoyer la votre à mailto:contact@net7.dev ou poser des questions si vous avez des difficultés.
¶ Algorithme à base de backtracking
Le but de cet algorithme est de visiter un chemin en suivant les directions (dans l'ordre) droite, haut, gauche, bas (l'ordre est sans importance, il faut juste un ordre de priorité). Et on emprunte la première qui est possible (présence d'une case libre et non d'un mur).
Si on se retrouve dans un cul-de-sac, on revient à la position précédente (le backtracking), et on marque la case actuelle comme chemin mort pour éviter de retourner dessus dans le futur.
En informatique, on garde en mémoire nos positions passées grâce à une pile. Celle-ci s'écrit en python en utilisant une liste pile = [] classique. On utilise les opérations pile.append(x) et x = pile.pop() pour manipuler la pile.
On testera cet algorithme avec le labyrinthe suivant (écrit avec la syntaxe python) :
# l’entrée est en haut à gauche
# et la sortie en bas à droite
M = [[0, 0, 0, 1, 0, 0, 0, 0, 1, 0],
[0, 1, 0, 1, 0, 1, 1, 1, 1, 0],
[0, 1, 0, 0, 0, 0, 0, 0, 1, 0],
[1, 1, 1, 1, 1, 0, 1, 1, 1, 0],
[0, 1, 0, 0, 0, 0, 1, 0, 0, 0],
[0, 0, 0, 1, 0, 1, 1, 0, 1, 0],
[1, 1, 0, 1, 0, 0, 1, 0, 1, 0],
[1, 1, 1, 1, 0, 1, 1, 0, 1, 0],
[0, 0, 0, 0, 0, 0, 0, 0, 1, 0]]
¶ Astuce ! Empêcher de sortir du labyrinthe
Afin d'éviter de traiter les cas où on peut sortir du labyrinthe comme des cas particuliers (risque de se tromper et rendre l'algorithme plus compliqué), on rajoute des murs tout autour du labyrinthe avec la fonction (syntaxe python) suivante :
def add_walls(mat):
wall_up_down = [[1]*(len(mat)+1)]
mat_with_walls_up_down = wall_up_down+mat+wall_up_down
mat_with_side_walls = list(
map(lambda liste: [1] + liste + [1],
mat_with_walls_up_down))
return mat_with_side_walls
Ce genre d'astuce est très commune en algorithmie pour éviter de gérer des cas particulier. On modifie les données de base (quitte à consommer plus de mémoire) pour ensuite simplifier l'écriture de l'algorithme.
ATTENTION !
Dans la nouvelle matrice (après ajout des murs) les cases de début et de fin subissent un décalage d'indice ! Il faut faire attention (en particulier pour notre condition d'arrêt).
¶ Correction proposée de l'algo de backtracking
On peut écrire cet algorithme en python sous cette forme :
def print_labyrinthe(M):
m = list(map(lambda liste: list(map(lambda x: 10*(1 - x), liste)), M))
m[0][0] = 5
m[-1][-1] = 5
matshow(m)
show()
def add_walls(mat):
wall_up_down = [[1]*(len(mat)+1)]
mat_with_walls_up_down = wall_up_down+mat+wall_up_down
mat_with_side_walls = list(
map(lambda liste: [1] + liste + [1],
mat_with_walls_up_down))
return mat_with_side_walls
# le paramètre debug permet d'afficher le labyrinthe
# modifié à chaque étape de l'algorithme
def labyrinthe(M, debug=False):
m = add_walls(M)
x, y = 1, 1
pile = []
while (x != len(m) - 2) or (y != len(m[0]) - 2):
m[x][y] = 5
if (m[x + 1][y] == 0):
x += 1
pile.append((1, 0))
elif (m[x - 1][y] == 0):
x -= 1
pile.append((-1, 0))
elif (m[x][y + 1] == 0):
y += 1
pile.append((0, 1))
elif (m[x][y - 1] == 0):
y -= 1
pile.append((0, -1))
else:
m[x][y] = 8
dx, dy = pile.pop()
x -= dx
y -= dy
if debug:
print_labyrinthe(m)
return m
On utilise les entiers :
- 0 pour une case libre
- 1 pour un mur
- 5 pour une case visitée (les 5 forment le chemin proposé à la fin de l'algorithme)
- 8 pour une « case morte »
Pour obtenir le chemin final, il suffit d'afficher le labyrinthe final et de regarder les cases avec des « 5 » ou de renvoyer le contenu de la pile.
On obtient (en animant ça avec matplotlib) :

Vous pouvez retrouver le code de la version animée dans l'archive de l'atelier 1
¶ Crible d'ératosthène
Le crible est un algorithme très classique et extrèmement utile permettant de lister tous les nombres premiers .
Son fonctionnement consiste à prendre la liste [0; 1; 2; …; N] des entiers naturels, puis on procède comme suit :
- On barre 0 et 1 car ils ne sont pas premiers
- On parcourt les nombres dans l'ordre jusqu'à
- Si ce nombre est barré, il n'est pas premier donc on continue
- Si ce nombre n'est pas barré, alors il est premier. On parcourt alors tous ses multiples dans la liste et on les barre
- Enfin on reparcourt la totalité de la liste pour lister les nombres qui sont pas barrés (donc premiers)
¶ Exemple d'implantation
def eratosthene(N):
m = [True]*(N+1)
m[0] = False
m[1] = False
i = 2
while i <= N/i:
if m[i]:
for k in range(2*i, N+1, i):
m[k] = False
i += 1
return m
m = eratosthene(97)
primes = []
for i in range(len(m)):
if m[i]:
primes.append(i)
print(primes)
REMARQUES :
- On utilise une liste de booléens pour indiqué si un nombre est premier ou non (n'est pas barré).
- On utilise l'indice de chaque élément de la liste pour savoir le nombre correspondant au booléen. On aurait pu commencer la liste à 2 pour économiser de la mémoire, mais cela aurait obligé à considérer des décalages d'indices dans tout le code (plus difficile à écrire, plus de risque de se tromper) donc on ne l'a pas fait.
- On utilise la condition
while i <= N / ipour éviter de calculer une racine carrée. C'est en effet une opération très couteuse qui apporte en plus des problèmes d'arrondi. On aurait pu écrirewhile i * i <= NMais cela nous oblige à travailler avec des nombres plus grand, ce qui peut amener des risques d'overflow dans certains langages.
(en effet, en python les entiers peuvent avoir des tailles arbitraires là où en C ils seront traditionnellement limités à des puissances de 2 selon le type d'entier)
¶ Bonus : Remarque sur l'écriture d'une matrice
Dans l'exercice du labyrinthe, nous avons eu à écrire des matrices. Nous avons choisi de l'écrire sous la forme d'un tableau de lignes.
Bien que cette représentation semble naturelle, elle n'est pas toujours si pertinente lorsqu'on travaille avec de très grosses matrices. Et c'est généralement pas la représentation utilisée par des bibliothèques de calcul matricielle comme Numpy ou des logiciels comme Matlab en raison de ses mauvaises performances sur de grandes matrices.
Remarque : Lors de compétitions comme le SWERC, l'utilisation de bibliothèques externes comme Numpy est interdite. Il est donc important de savoir écrire nos propres matrices sans bibliothèque de façon performante.
¶ Pourquoi faire des tableaux de tableaux c'est pas toujours idéal ?
Les listes de listes offrent une façon pratique pour le programmeur de manipuler des matrices. Il est en effet naturel, et proche de l'approche mathématique d'écrire M[i][j] pour accéder à l'élément d'indice .
Cependant, cela oblige d'allouer l'espace mémoire des lignes de la matrice en plusieurs fois. Pour créer la matrice nulle de taille , on doit faire une boucle :
n = 3
m = 2
M = []
for i in range(n):
M.append([0] * m)
print(M)
La création de la matrice est donc en complexité linéaire en le nombre de lignes !
ATTENTION : Vous pouriez être tenté d'écrire M = [[0] * m] * n mais c'est totalement faux !!!!
Essayez d'écrire M[1][1] = 2 et regardez le résultat (toutes les lignes sont modifiées et non uniquement celle d'indice 1).
Second problème :
L'autre soucis de la représentation sous forme de listes de listes, c'est que les éléments de deux lignes qui se suivent peuvent avoir des adresses mémoires très éloignées !
(en effet, comme il s'agit de 2 tableaux différents, leurs éléments n'ont aucune obligation d'être à la suite dans la RAM de l'ordinateur).
De manière générale, deux allocations de ressources à la suite, ne sont jamais à la suite au niveau physique, dans la mémoire de l'ordinateur.
Ce désordre dans la mémoire de l'ordinateur empêche la mise en place de beaucoup d'optimisations au niveau du processeur. Ce dernier à en effet tendance à mettre en cache (dans une mémoire beaucoup plus petite et rapide que la RAM) des valeurs qui se suivent en mémoire. Cela lui permet d'y accéder plus tard beaucoup, beaucoup, beaucoup plus rapidement que s'il doit relire la RAM.
Avec plusieurs tableaux différents, on augmente extrèmement fortement les risques de défaut de cache (vous verrez plus en détails ce problème lors des cours d'architecture des ordinateurs et de calcul scientifique).
¶ Solution performante pour représenter des matrices
La solution, c'est donc de faire une seule allocation de mémoire pour l'ordinateur. Donc d'utiliser un seul tableau !
On va donc concaténer les lignes de notre tableau les unes à la suite des autres dans un unique tableau de taille .
Remarque : Selon l'algorithme à implanter, il peut être plus pertinent d'écrire sous forme de concaténation de colonnes afin que 2 éléments de la même colonne soient plus proches dans la mémoire (voir les cours de calcul scientifique au S7)
L'allocation de la matrice se font donc sans boucle comme suit :
M = [0] * (n * m)
Et l'accès à l'élément d'indice s'écrit avec l'opération :
element = M[i * n + j]
Il peut être judicieux d'écrire une fonction pour accéder à l'élément d'indice pour éviter de se tromper.